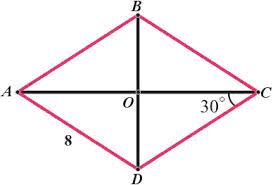
Bizonyítsuk be, hogy a gyémánt 1
lecke Célok
• Továbbra is megismertesse a hallgatókat egy geometriai alak, mint a gyémánt;
• Rögzítse a tudás fogalmak, mint a gyémánt és szögletes, valamint megtanulják, hogyan kell meghatározni a különbség;
• Frissítés ismerete iskolások a tulajdonságait és jellemzőit a rombusz;
• Folytatni kell a tanulók tudását geometriai alakzatok a folyamat problémák megoldásához.
• Hívás az érdeklődés a geometria órák.
lecke célkitűzések
• Ismétlés, összefoglalja és megszilárdítsa tudásukat egy geometriai alak, mint a gyémánt;
• Továbbra is generál képességek építése geometriai alakzatok között;
• A készségeinek javítására építési rombusz segítségével rajzeszközök;
• Továbbra is megszilárdítsa tanulók tudását a gyakorlati feladatokat;
• további fejlesztése a figyelmet, a szorgalom és az elkötelezettség a kognitív folyamat.
óravázlat
1. Tájékoztatás a fő tanulsága a téma, a meghatározása egy geometriai alak „Diamond”.
2. Bevezetés a tulajdonságok és funkciók a rombusz.
3. tételek és bizonyítások.
4. Hogyan kell felhívni a gyémánt. Módszerek rombusz képet.
5. Hogyan lehet megtalálni a területet a rombusz?
6. Ismétlés tartozó anyag.
7. Érdekes tények.
8. Házi.
Meghatározása a rombusz, mint a geometriai alakzat
Rhombus - paralelogramma amelynek minden oldala egyenlő. Ha a gyémánt szögletes sarkok, ez az úgynevezett egy négyzet.
A „cukorka” fordították a görög jelentése „dob”. Természetesen, hogy megértsük a gyémánt, mint egy hangszer, van egy kör alakú. De ez most teszi a gyémánt kerek, és a régi időkben, csak volt egy négyzet alakú vagy rombusz alakú.
Nézzük alapmeghatározásait rombusz, és próbálja megérteni, mi ez a mértani alakzat.
Rhombus - ez olyan egyenlő oldalú paralelogramma, melynek egyenlő oldalú, de egyenlőtlen szögek.
Rhombus és feltételezhetjük, egy egyenlő oldalú négyszög, amelynek két átellenes hegyesszög és két tompaszög.
Ezzel szemben a négyzet, a rombusz - egyenlő oldalú rombusz.
Mint mindig van számos definíciója változó geometriai formák, de ez nem jelenti azt, hogy minden tanulónak, hogy üljön le, és „memorizálni” ezek a meghatározások. A különbség a definíciók - ez milyen széles körben írják le a geometriai alakzat. A legfontosabb dolog az, hogy megértsük, mit mondanak a meghatározása és a lehetőséget, hogy a szám. Ha követed a két szabályt, te magad is képes írni, vagy adjunk hozzá egy pár definíciók.
tulajdonságait egy rombusz
1. Az első jellemzője a rombusz tekinthető, hogy a gyémánt egy téglatest, mint ellentétes oldalai párhuzamosak, AB // CD, AD // BC.
2. A második a tulajdonságai, hogy az összes átlói metszik rombusz derékszögben. A metszéspontja az átlók rombusz felezővonal.
3. A szögfelezői szögek a rombusz az átlós.
4. Ahhoz, hogy megtalálja a négyzetének összege a átlói rombusz, szükséges, hogy szaporodnak a tér oldalán négy.
5. ellentétes oldalain a rombusz egyenlő;
6. A szögeinek összege a rombusz, amelyek szomszédosak az egyik oldalán, a 180 fok.
jelei a rombusz
A paralelogramma, rombusz az esetben, ha megfelel a következő feltételeknek:
1. Először is, ő minden oldala egyenlő egymással;
2. Másodszor, átlói metszik rombusz derékszögben.
3. Harmadszor, ha az átlók a sarkok bisectors.
4. A negyedik, ha két szomszédos oldala egyenlő.
5. Az ötödik, ha legalább az egyik átló felezi a paralelogramma.
Tételek és bizonyítások
Most vessünk egy közelebbi pillantást a tulajdonságait és jellemzőit egy rombusz, bizonyítva a tételt:
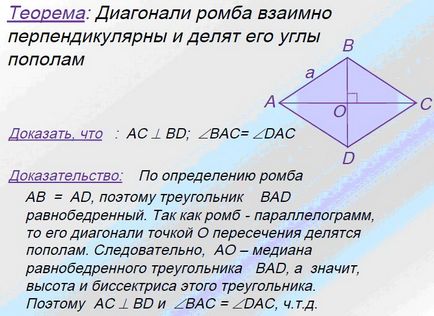
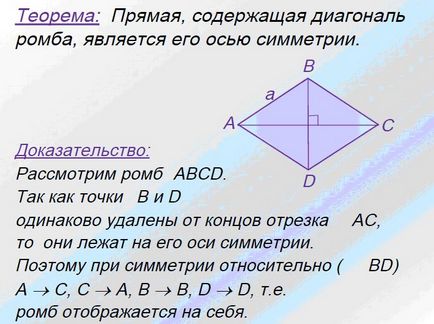
Ebből az következik, hogy:
1. rombusz két szimmetriatengelye - képátlónál AC és BD.
2. A átlók merőlegesek egymásra.
3. A szintén szögfelezői szöge.
A terület rombusz
A terület a rombusz felével egyenlő a termék átlók. De mint a gyémánt, sőt, paralelogramma, a terület megtalálható szorozni kézzel a magasság.
Formula területe rombusz:
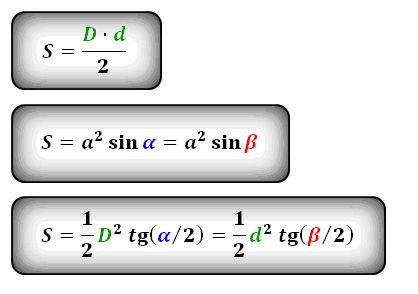
Ahol: a - a fél a rombusz
D - jelöli a nagy átlós
d - nevezzük alacsonyabb átlós
α - egy hegyesszög
β - ez tompaszögben
A terület bármilyen geometriai alakja része a felület által definiált zárt hurok az ábra. A értéke a rombusz terület kifejezett száma négyzet álló egységek benne.
Hogyan kell felhívni a gyémánt
Felhívni a rombusz tulajdonságainak használata az átlók rombusz. Azt már tudjuk, hogy a diagonális geometriai formák merőlegesek és felezik a metszéspont. Ezért az építkezés egy rombusz legkönnyebb kezdeni az építési átlók.
És így, először válassza ki azt a pontot, ahonnan már elhalasztják a bal és jobb oldali részek azonos hosszúságú azonos fel és le a hosszát a többi szegmens.
Most már csak csatlakoztatni kell a végén ezeket a szegmenseket, és ennek eredményeként kapunk egy gyémánt.
Rombusz is felhívni használata nélkül átlók. Ebben az esetben azt kell meghatározni, csak a végén a átló, majd csatlakoztassa a pontok vonalak.
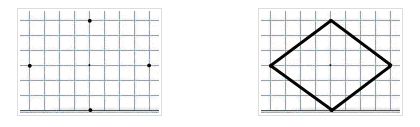
Végül a harmadik út rajz rombusz lehet végezni egy vonalzóval. Mivel mindannyian tudjuk, hogy a gyémánt van egyenlő oldalú, akkor először meg kell rajzolni az alján. Ezután meg kell halasztani az egyenlő szegmensét is. És mint egy harmadik fél, párhuzamosan az első, az összekötő végei az első és a harmadik szegmenst, akkor egy gyémánt.
ismétlés
Ön már ismeri a geometriai alak, mint a gyémánt, és tudja, hogy egy négyzet egy speciális esete is.
1. Ezért Idézzük a meghatározása, hogy mi a tér? Adj magadnak a meghatározása a téren.
2. Milyen tulajdonságai a tér? Hívja őket.
3. Mi a különbség a gyémánt és a tér, a tér, ha ez egy különleges eset?
4. Milyen szám az úgynevezett négyszög, és ha egy gyémánt utal, hogy a geometriai alakzat?
5. Milyen típusú négyszögek tanultál? Hívja őket.
6. Mi a különbség a kettő között?
Érdekes tudni, hogy
Tudtad, hogy ha veszi a dobozt és csatlakoztassa a felezőpontja az oldalán, akkor a végén egy gyémánt.
És ha éppen ellenkezőleg, elvisszük a gyémánt, és megpróbál csatlakozni, hogy a felezőpontja a szegmensek, megkapjuk a geometriai forma, mint egy téglalap.
Ha veszel egy paralelogramma egyenlő magasságú, akkor ez a paralelogramma rombusz.
érdekes tények
Tudtad, hogy a nevét, a kártya ruha gyémánt, amelynek rombusz alakú megjelent a nap, amikor a tambura korántsem volt kör alakú, és formájú rombusz vagy négyzet.
Ez az első alkalom a „gyémánt” az ő lexikon használták Herron és Papposz.