Rombusz, trapéz - a tanulmány a témában - sokszögek - az iskolai geometria tanfolyam

A tankönyv „Geometry 7-9” LS Atanasyan (4) A „gyémánt” bevezetjük §3 46. igénypont szerinti „Diamond és tér”: rombusz hívják egy paralelogramma, amelyben minden oldalról egyenlő. További felülvizsgálat, és bizonyítani, rombusz tulajdonság: „Az átlói merőlegesek rombusz és elosztjuk a két sarkában.”

AV Pogorelov (18) a témája a "rombusz" azonosítja egy adott elem (55).

Az elején a bekezdés meghatározza: Rombusz - paralelogramma, amelynek minden oldala egyenlő. És akkor belép a rombusz tulajdon tétel 6,5: „Az átlói metszik rombusz derékszögben. Átlói rombusz a szögfelezői szöge. "

AC, BD - átlósan.

AC, BD - felezővonal.

AABC - egyenlő szárú, mert AB = BC (ABCD-gyémánt).

AO = OS (a tulajdonsága paralelogramma) => IN - Medián, a => és a szögfelező, és a magasság.

Tehát BD - felezővonal B és merőleges az AU.

Tekintsük a módszer tanulmányozása a témája a „Diamond” a tankönyvi példa AV Pogorelov.

Bevezetése után az ingatlanok és meghatározásokat a rombusz diákok megoldani a problémákat.

1. feladat. Bizonyítsuk be, hogy ha az átlók paralelogramma merőlegesek, akkor ez egy rombusz.

Adott: ABCD paralelogramma-, AC, BD-átló, acbD.

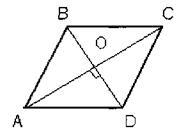
Hagyja Mintegy - a metszéspontja az átlók. # 63; AOB = # 63; AOD (alapján I), AOB = AOD = 90 (a feltételezés) OA - általános, OB = OD (tulajdonság az átlók a paralelogramma).

=> AB = AD. És az ingatlan ellentétes oldalán a paralelogramma AD = BC, AB = CD.

3adacha 2. Kerülete rombusz ABCD 56cm. Keresse rombusz sarkok (szájon át).

3adacha 3. Az egyik a sarkokban a rombusz egyenlő 72. ABCD kap rombusz sarkok (orálisan).

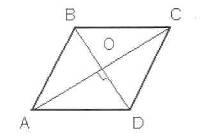
Válasz: A = C = 72, B = D = 108.

Akkor tudnak kínálni rendszer feladatok:

1. ABCD rombusz tartott AC átló. Bizonyítsuk be, hogy az ABC háromszög - egyenlő szárú.

2. Két kör középpontja O és O1 egyenlő sugarú és metszéspontjai A és B Mutassuk meg, hogy a négyszög AO1 VO - paralelogramma.

3. Side rombusz van 18 cm, és egyik szöge megegyezik a 150 kap a távolságot a szembenálló felek.

4. Bizonyítsuk be, hogy a metszéspont a átlói rombusz egyenlő távolságra van az oldalán.

A tankönyv „Geometry 7-11” AV Pogorelov (18) témája az „A-Line” tanulmányozták 6.§ követelés 59 „trapéz”. Meghatározása a trapéz bevezetjük nachalepunkta: trapéz hívják négyszög, amelyben csak két szemközti oldalai párhuzamosak. Ezek a párhuzamos oldalai nevezzük alapjai a trapéz. A másik két oldala pedig az úgynevezett oldalát.

Következő bevezette a „egyenlő szárú trapéz” és „a középső sor a trapéz”, és ezt tartják tétel 6,8 (a középvonal a trapéz): „A középső sor párhuzamos bázisok a trapéz és felével egyenlő summája.”

A tankönyv „Geometry 7-9” LS Atanasyan (4) a „trapéz” bevezetjük §2 «paralelogramma és trapéz” 44. pontjában az »A-line«:

„Keystone úgynevezett négyszög, amelynek két oldala párhuzamos, másik két oldala nem párhuzamos. Párhuzamos oldalai trapéz nevezzük annak alapjait, és a másik két fél - az oldalán.

Trapéz úgynevezett egyenlő szárú, ha megegyeznek. Trapéz, egyik sarkában, amely egy egyenes vonal, az úgynevezett téren. "

Tekintsük a módszer tanulmányozása a témája a „Keystone” a tankönyvi példája AV Pogorelov.

Trapéz úgynevezett négyszög, melynek csak két szemközti oldalai párhuzamosak. Ezek a párhuzamos oldalai nevezzük alapjai a trapéz. A másik két oldala pedig az úgynevezett oldalát.

Itt látható trapéz ABCD bázisokkal AB és CD, valamint a BC oldalon és AD felekkel.

Trapéz, amelyek az úgynevezett oldalán egy egyenlő oldalú. Összekötő szakasz közepén a fél, az úgynevezett középső sor a trapéz.

Tétel 6.8: A középső sor párhuzamos bázisok a trapéz és felével egyenlő summája.

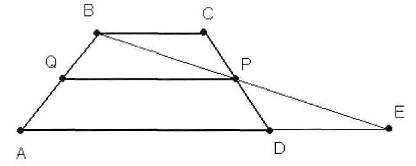
BP # 63; AD = E, # 63; PBC = # 63; PED (a második jellemző az egyenlőség háromszögek) CP = DP (az építési), PCB = PDE (belső keresztben fekvő párhuzamos vonalak a BC és az AD és a vágási CD), BPC = EPD (függőleges).

A egyenlőségét háromszögek => = PB PE, BC = ED.

Tehát a középső sor PQ középvonala a trapéz # 63; AVE. Szerint a tulajdonságok a közepes vonal a háromszög PQ || AE és a szegmens

pq = # 63; AE = # 63; (ad + bc).

Bevezetése után a fenti fogalmak diákok megoldani a problémákat.

Zadacha1. A trapéz ABCD sarkok szomszédos oldalán a AD, 74 és 81. Határozzuk meg a szögek szomszédos oldalán a Nap (Per os).

Válasz: ABC = 106, BCD = 99.

Zadacha2. Igazoljuk, hogy egy egyenlő oldalú trapéz szögek tövénél egyenlő.

Adott: ABCD egyenlő szárú trapéz,

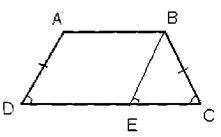
BP || AD, Abed - paralelogramma => BE = AD (a tulajdonsága paralelogramma) AD = BC (a hipotézis) => # 63; ALL - egyenlő szárú EU-alapon. A sarkok a háromszög és a trapéz, a vertex C azonosak, és a szögek a vertex E és D mindkettő a kereszteződésekben a megfelelő sarkait metsző párhuzamos vonalak. Ezért ADC = BCD.

Ezután a diákok hez rendszer célzó feladatok megfelelő készségek fejlesztésére.

1. Egy egyenlő oldalú trapéz ABCD sarkok szomszédos AD oldal, egyenlő 45. megtalálni a trapéz magassága, ha az alap 13 cm és 27 cm.

Bizonyítsuk be, hogy ha az átlók egyenlő a trapéz, trapéz egyenlő szárú.

A trapéz, okok egyike, amely egyenlő 5 cm tartott a középső sor, amelynek hossza megegyezik 6 cm. Mi a másik alapja a trapéz?

A átlói metszik a trapéz ABCD RP átlagos vonal pontok M és N. Igazoljuk, hogy RM = NP.

Bizonyítsuk be, hogy a felezőpontja egy egyenlő oldalú trapéz csúcsai rombusz.

Áttekintés lecke „trapéz. A középső sorban a trapéz "

Oktatás: megszilárdítsa a tudás a vizsgált tulajdonságok a trapéz és a tételt az középvonalban a trapéz, trapéz tanítani feltételek meghatározása létezik; megtanulják, hogyan kell alkalmazni a képlet a megállapítás a középső sor a trapéz meg egyszerű feladatokat, valamint a hasonló helyzetek, új.

Fejlődő. készségek fejlesztése az önkontroll és a kölcsönös ellenőrzés, a fejlesztési logikus gondolkodás, a hozzáértő és gondos kivitelezés.

Nevelési: oktatás a függetlenség és kollektivista kultúra beszédet.

Felszerelés: 2 fél lapot, és 1 másolati laptól, minden diák írószer, számviteli mérleg minden tanuló számára.

1. megszervezése leckét.

Bevezetése előtt meg kell határozni az trapéz hasznos felidézni a meghatározása a paralelogramma és, hogy ezt a fajta négyszög, melynek csak két szemközti oldalai párhuzamosak. (Meghatározása a trapéz kíséri egy mintát a táblán).

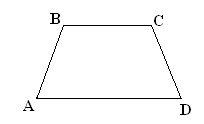
2. rögzítése a koncepció a trapéz kész keresztül rajzokat a fedélzeten, és számít nekik:

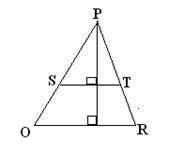
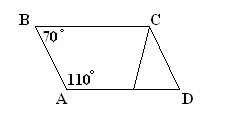
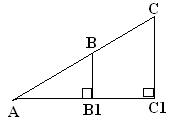
1) Melyik téglalapok ábra. a), b), c) egy trapéz?

Hívja őket a bázis és az oldala.

A trapéz MNRK tartott szegmens PE // MN. Határozza meg a négyszög MNRE.

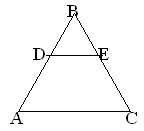
Az egyenlő oldalú ABC háromszög oldalai 8 cm tartott a középső vonal DE. Határozza meg a négyszög ADES. Mik az oldalán a négyszög?

Tekintsük elemek és hívja trapéz trapéz faj.

3. Mérlegelni igazolás a középvonal a trapéz.

Az előadás után a bizonyítás célszerű rögzíteni a következő lépéseket:

Hozzáépített: szegmens BE;

RO - középső sorban megduplázása.

Következtetés: PO // AD, PO = 1/2 (AD + BC)

Megjegyzés: (EP - a középső sor a trapéz, a szegmens PO - lehet tekinteni, mint megduplázva a középvonaltól)

4. A kezdeti konszolidációs a középvonal tétel megy keresztül egy megoldás a típusú problémák:

1) A bázisok a trapéz 7 és 9 cm. Mi a középső sor a trapéz?

MN - középső sorban trapéz ABCD. . Miután N t tartott párhuzamos vonalban, az AB oldalt és az oldalsó AD metszi P pontban Igazoljuk, hogy MNRA - paralelogramma.

3) Egy trapéz ABCD ismert mellékhatások: AB = 4 cm, BC = 6 cm, CD = 5 cm, AD = 10 cm Mik az oldalán a trapéz AEFD, ha EF - a középső sor a trapéz.?

Mind a oldalán a trapéz ABCD van osztva négy egyenlő részre. Mik a szegmensek M N. M N és M N, ha az AD = 11 cm, BC = 3 cm?

5) a Moldovai Köztársaság - a középső sor a trapéz ABCD bázisokkal AD és BC = a = c. Ez áthalad az AC átló a C. Mik hosszát a Kazah Köztársaság és a kabinet?

6. A középső sorban a trapéz egyenlő 8 cm, és az egyik oka 6 cm. Mi más okból?

Biztonságossá az új anyag a javasolt feladat, azt mutatja - a megértett és megtanult új anyag.

5. Összegezve a leckét:

- A nevek elemében;

- készítményt a tételnek a középvonal.

Nyilatkozat házi :. 59. § p 92-93, 17-19 kérdései ass. №59 100.o..

Ellenőrzése a asszimilációja anyaggal végzett teszteléssel (feltételezve, hogy a differenciált szabályozása diákok tudásának).

A kötelező része kedvezmény feladatok sikeres végrehajtása érdekében, amely a diákok kell használni a minimális tudásszintet a szoftverre vonatkozó követelményeknek. További része tartalmazza a két feladat az átlagos szint a komplexitás, ami megfelel a legtöbb fő feladata a tankönyv, és két feladat haladó diákok számára.

Az ehhez szükséges idő vizsgálat alapján határozzák meg a képességeit egy adott osztályban.

1) (1) Töltse ki az üres, hogy a megfelelő nyilatkozatot.

A középső sor párhuzamos a bázisok a trapéz és _____________

2) (1) Ha a MN - középső sorban trapéz ABCD, akkor a hossza egyenlő MN ________________________________________________

AD és BC - a bázis a trapéz.

3) (2) A igaz vagy hamis voltát a következő állítások:

A) A összekötő szakasz az oldalán a trapéz, nevezzük annak középvonala ________________

B) Ha a bázis a trapéz 4 cm és 8 cm-es, a középső sor 4 cm ___________________

a) 7 cm; b) 5 cm; c) 3 cm.

5) (3) Az egyik a trapéz bázisok hosszabb további 2 alkalommal. A középső sor a trapéz = 15 cm. Megtalálja a bázist.

a) 5 cm; 10 cm; b) 10 cm; 20 cm; c) 15 cm; 30 cm.

6) (3) A kisebb alapja a trapéz tárgya a közepes hálózati, mint 2: 3. Get kisebb bázis hosszát, ha a nagyobb alap legalább 16 cm.

a) 8 cm; 12 cm; b) 10 cm; 15 cm; c) 4 cm és 6 cm.

(4) Tekintettel: ABCD - trapéz. AM = BM, BN = ND. Bizonyítsuk be, hogy MP - középső sorban a trapéz ABCD.

8) (4) Midline trapéz 2 cm-rel kisebb, mint a nagyobb bázist. Keresse meg a középvonala a trapéz, ha a kisebb bázis 6 cm.

a) 8 cm; b) 10 cm; c) 5 cm.

9) (5) egy egyenlő szárú trapéz ABCD merőleges csökkent a vertex V nagyobbik alapja BD, osztja azt egy intervallum egyenlő 4 cm és 7 cm. Ki az átlagos vonal és a kisebb alapja a trapéz.

a) 10 cm; b) 4 cm; c) 8 cm.

10) (5) egy egyenlő szárú trapéz ABCD MN - középső sorban, BC = 6 cm, 14 cm-es MN = Számítsuk ki a hossza a szegmens, amely része a középvonal és a között az átlók a trapéz hazugság ..

a) 10 cm; b) 4 cm; c) 8 cm.