Regresszióanalízis - a statisztikai módszer vizsgálja a függőség a véletlen változó által

előző ◈ a következő

A statisztikai regressziós analízis modellező tanulmány értékelésére használják a változók közötti kapcsolatban. Ez a matematikai módszer magában foglal több más módszerek modellezésére és elemzésére többváltozós, amikor a hangsúly a kapcsolat a függő változó, és egy vagy több független. Pontosabban regressziós elemzés segít megérteni, hogy a jellemző értéke a függő változó, ha a független változók változik, míg a többi független változó rögzítve van.

Minden esetben a cél pontszámot függvénye a független változók az úgynevezett regressziós függvény. A regressziós analízis is érdekes, jellegzetes változások, mint a függő változó, a regressziós függvény, amely leírható egy valószínűségi eloszlás.

Feladatok regresszió analízis

A statisztikai módszer a kutatás széles körben használják, hogy előre, ha annak használata jelentős előnyökkel jár, de ez néha vezethet hamis kapcsolat illúzió, vagy így ajánlott használni pontosan ebben a kérdésben, hiszen például a korreláció nem jelent ok-okozati összefüggés.

Ez kifejlesztett számos módszer kivitelezésére egy regressziós elemzést, például a lineáris regresszió és a legkisebb négyzetek, amelyek parametrikus. Ezek lényege, hogy a regressziós függvény meghatározása a véges számú ismeretlen paraméterek, amelyek az adatokból becslés alapján. Nonparametrikus regressziós függvény lehetővé teszi, hogy feküdjön egy bizonyos függvények halmazát lehet végtelen dimenziós.

Ennek statisztikai módszer tanulmányozására, regressziós elemzés a gyakorlatban alakjától függ generáló folyamat, és hogyan kapcsolódik a regressziós megközelítés. Mivel az igazi formáját eljárás adatai, áramfejlesztő, mint általában, egy ismeretlen szám, regresszió analízis gyakran attól függ, hogy bizonyos mértékig feltételezések a folyamatot. Ezek a feltételezések néha ellenőrizhető, ha van elég adat. Regressziós modellek gyakran hasznos, ha a feltételezések mérsékelten sérülnek, bár nem működik maximális hatékonysággal.

Szűkebb értelemben regresszió is kifejezetten a becslés folytonos válasz változók, ellentétben a diszkrét választ használt változók a címkézés. A folyamatos kimeneti változó is nevezik mutató regressziós, hogy megkülönböztessék a kapcsolódó problémák.

A „regresszió” Francis Galton találta a XIX leírni egy biológiai jelenség. A lényeg az volt, hogy a növekedés a leszármazottai az ősök a növekedés általában visszafejlődnek le a normál átlag. Mert Galton regresszió már csak ez a biológiai értelme, de később a munka folytatódott Udni Yoley és Karlom Pirsonom és visszavont, hogy minél több általános statisztikai összefüggésben. A munkát a Yule és Pearson együttes eloszlása a magyarázó változók és a válasz minősül Gauss. Ezt a javaslatot elutasította Fisher a munkálatok 1922-ben és 1925. Fisher azt javasolta, hogy a feltételes eloszlása a válasz változó Gauss, de az együttes eloszlás nem kell. Ezzel kapcsolatban feltételezés Fischer közelebb szövegéből 1821 Gauss. 1970 előtt néha vett akár 24 órát is, hogy az eredmények a regresszió analízis.

Módszerek regressziós elemzés továbbra is aktív kutatási terület. Az utóbbi évtizedekben, új módszert dolgoztak ki a megbízható regresszió; regressziós korrelált válaszokat; regressziós technika befogadására különböző hiányzó adatok; nonparametric regresszió; Bayes regressziós módszerekkel; regresszió, amelyben a változók prediktív mérési hiba; Regresszió a legtöbb előrejelzője, mint megfigyelések és az oksági következtetés a regresszió.

regressziós modellek

Összes regressziós elemzés tartalmazza a következő változókat:

Az ismeretlen paraméterek jelölve béta, ami lehet egy skalár vagy vektor.
Független változók, X.
A függő változó, Y.

A különböző területeken a tudomány, ahol a használata regressziós elemzést végeztünk, a különböző használt kifejezések helyett függő és független változók, de minden esetben a regressziós modell tárgya az X és Y funkció β.

A közelítés általában készült formájában E (Y | X) = f (x, β). Végrehajtásához regressziós elemzést kell meghatározni formájában az f függvény. Ritkábban, ez alapján a tudás közötti kapcsolat Y és X, ami nem adatokra támaszkodnak. Amennyiben ez a tudás nem áll rendelkezésre, válasszuk ki a rugalmas és kényelmes forma F.

A függő változó Y

Tegyük fel most, hogy a vektor ismeretlen paramétereket β hosszúsági k. Ahhoz, hogy végre regresszió analízis, a felhasználónak meg kell adjon tájékoztatást a függő változó Y:

Ha N adatpontok az űrlap (Y, X), ahol N

Ha vannak pontosan N = K, és az F függvény lineáris, az egyenlet Y = F (X, β) meg lehet oldani, hogy pontosan és nem hozzávetőlegesek. Ez csökkenti a megoldása egy sor egyenletek N-N-ismeretlennel (az elemek P), amelynek van egy egyedülálló megoldás, ameddig X jelentése lineárisan független. Ha F egy nemlineáris, a megoldás nem létezik, vagy lehet, hogy sok megoldásokat.
A leggyakoribb helyzet ott, ahol N> pont az adatokat. Ebben az esetben elegendő információ az adatok értékeléséhez az egyedi érték β, amely a legjobban illeszkedik az adatokra, és a regressziós modell, ahol az alkalmazás adatait lehet tekinteni, mint egy túlhatározott rendszer β.

Az utóbbi esetben a regresszió eszközöket biztosít:

A megoldások keresése az ismeretlen paramétereket β, amelyet, például, hogy minimálisra csökkentsék a távolságot a mért és a számított értéke Y.
Bizonyos feltételek mellett a statisztikai regressziós analízissel fölös információt nyújt statisztikai információt az ismeretlen paramétereket p és becsült értékek a függő változó Y.

A szükséges számú független mérés

Tekintsük a regressziós modell, amely három, ismeretlen paramétereket: β0. β1 és β2. Tegyük fel, hogy a kísérletvezető végez 10 mérést egy és ugyanazon érték a független változó vektor X. Ebben az esetben, regressziós elemzés nem ad egy egyedülálló értékek. A legjobb, ami történhet, hogy megbecsüljük a átlaga és szórása a függő változó Y. Hasonló módon mérjük két különböző értékei X kaphat elegendő adat a regresszió két ismeretlen, de nem három vagy több ismeretlen.

Ha a méréseket kísérletvezető végre három különböző értéket a független változó X vektort, a regressziós analízis nyújt egy egyedülálló a pontszámok a három ismeretlen paramétereket β.

Abban az esetben, általános lineáris regressziós állítás egyenértékű azzal a fenti követelmény, hogy a mátrix X T X reverzibilis.

statisztikai feltevések

Ha a mérések száma N nagyobb, mint ahány ismeretlen paramétereket k és hiba eí méréseket. ez általában kiterjed majd fölös szereplő információk a méréseket, és használják a statisztikai előrejelzéseket az ismeretlen paramétereket. Ez a többlet információt az úgynevezett szabadsági foka a regresszió.

feltevéseket

Klasszikus feltételezések regressziós elemzés a következők:

A minta reprezentatív következtetés predikciós.
A hiba egy véletlen változó, az átlagos értéke nulla, amelynek feltétele a magyarázó változók.
A független változók mérése hiba nélkül.
A független változók (prediktorai) lineárisan független, azaz nem lehet kifejezni bármilyen prediktor lineáris kombinációjával a többiek.
Hibák korrelálatlanok, vagyis a kovariancia mátrix diagonális hibákat, és minden nem nulla eleme van a hiba variancia.
Hibavariancia állandó megfigyelésekből (homoszkedaszticitás). Ha nem, akkor a súlyozott legkisebb négyzetek vagy más módszerekkel.

Ezek elégséges feltételei legkisebb négyzetek becslési rendelkezik a szükséges tulajdonságokkal, különösen feltételezések jelenti, hogy a paraméter becslések torzítatlan, következetes és hatékony, különösen, ha azok regisztrálva az osztály a lineáris becslések. Fontos megjegyezni, hogy bizonyítékokat ritkán kielégíteni. Vagyis a módszert alkalmazzuk, akkor is, ha az a feltételezés nem helyes. Változik a feltételezések néha használni, mint egy intézkedés mutatja, hogy ez a modell hasznos. Sok ilyen feltételezések lehet enyhíteni a fejlettebb technikák. Reports statisztikai elemzés jellemzően elemzését vizsgálati mintán a módszertan és használati mintaoltalmi.

Ezen túlmenően, a változók bizonyos esetekben utalnak mért ponton helyszíneken. Lehetnek térbeli trendek és térbeli autokorreláció a változók, amelyek sértik a statisztikai feltételezéseket. Földrajzi súlyozott regresszió - az egyetlen módszer, hogy köze van az adatokat.

Lineáris regresszió analízis

A lineáris regresszió jellemző, hogy a függő változó, amely nem Yi. Ez jelenti a lineáris paraméterek kombinációja. Például, egy egyszerű lineáris regressziós modellezést n-pontokat alkalmazunk, az egyik független változó, xi. és két paraméter, β0 és β1.

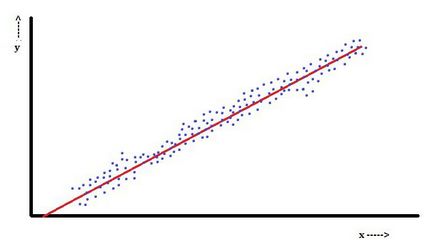
A többszörös lineáris regresszió, több független változó vagy függvény.

Amikor egy véletlen minta a népesség a paraméterei lehetővé teszik, hogy olyan mintát kapjunk egy lineáris regressziós modellben.

Ebben a vonatkozásban, a legnépszerűbb a legkisebb négyzetek módszerével. Ezzel kapott értékelési kritériumok, amelyek minimalizálják a négyzetesen összegzett maradékok összege. Ez a fajta minimalizálási (karakterisztika lineáris regresszió) Ennek a funkciónak vezet egy sor normál egyenletek, és egy sor lineáris egyenletek paramétereket, amelyeket megoldani becslést kaphatunk a paraméterek.

A további feltételezés, hogy a lakosság normális eloszlású hiba, a kutató használhatja ezeket a becsléseket standard hibák létrehozását megbízhatósági határokat és vizsgálati hipotézisek paramétereit.

Nemlineáris regresszió analízis

Egy példa, ahol a függvény nem lineáris tekintetében paraméterek, azt jelzi, hogy a négyzetösszeg minimalizálni kell egy iteratív eljárás. Lehetővé teszi, hogy egy csomó komplikáció, amely meghatározza a különbség a lineáris és nem lineáris legkisebb négyzetek módszerével. Következésképpen, az eredmények a regresszió a nemlineáris eljárás néha kiszámíthatatlan.

Kiszámítása teljesítmény és mintanagyság

Itt is, mint általában, de nincsenek rögzített módszerek kapcsolatos esetek száma, mint a független változók száma a modellben. Az első szabály javasolták Jó és Hardin és úgy néz ki, mint az N = T ^ n, ahol N a minta mérete, n - a független változók száma, és t a megfigyelések száma eléréséhez szükséges a kívánt pontosságot, ha a modell csak egy független változó. Például, egy kutató épít lineáris regressziós modell alkalmazásával adatkészlet tartalmazza 1000 beteg (N). Ha a nyomozó úgy dönt, hogy ötször kell megfigyelések, hogy pontosan a vonal (m), a maximális számú független változó, amely a modell is támogatja a 4.

más módszerek

Annak ellenére, hogy a paramétereket a regressziós modell általában becslések a legkisebb négyzetek módszere, vannak más módszerek, amelyek sokkal ritkábban. Például, a következő módszerek:

Bayes technikák (például, Bayes lineáris regressziós módszer).
Érdeklődjön regresszió olyan helyzetekben, ahol a visszaesés érdeke hibák a megfelelőbb.
A legalacsonyabb abszolút eltérés, hogy sokkal stabilabb jelenlétében kibocsátás, ami a kvantilis regresszióval.
Nonparametrikus regresszió, amely megköveteli a nagy számú megfigyelések és számítások.
A távoktatás mutatókat, amelyek tanulmányozták a keresést egy értelmes mutató távolság a megadott bemeneti térben.

szoftver

Minden nagyobb statisztikai szoftvercsomag segítségével végezzük a legkisebb négyzetek regressziós analízissel. Egyszerű lineáris regresszió és a többszörös regressziós analízis alkalmazható egyes alkalmazások, táblázatok, valamint néhány számológépek. Bár sok statisztikai szoftvercsomag végezhet a különböző típusú, nem paraméteres és robusztus regresszió, ezek a módszerek kevésbé szabványosított; Különböző szoftvercsomagok a különböző módszereket. Specialized regressziós szoftver került alkalmazásra fejlesztették ki olyan területeken, mint a végzett felmérés és a képalkotó.