Prism (geometria)

Csoport n -ugolnoy szimmetria egyenes hasáb, amelynek a megfelelő bázis a csoport Dn h 4n érdekében. azzal az eltéréssel, kocka, hogy van egy szimmetria csoport Ó [en] a sorrendben 48, amely tartalmaz három változatban d4h mint alcsoportok. Forgatás csoport [en] DN rend 2n. kivéve abban az esetben, egy kocka, amelyre a forgatás csoport O [en] a sorrendben 24, amelynek három változata D4, mint alcsoportok.

Csoport Dn h szimmetriát tartalmaz egy központi szimmetria és csak abban az esetben, ha n páros.

Prismatic poliéder - a szintézist prizma a terek a 4. dimenzió és a fenti. n dimenziós poliéder prizma van kialakítva két (n - 1) dimenziós poliéder átvezetik a következő dimenzióba.

Elements n dimenziós poliéder prizma kettős elemek (n - 1) dimenziós poliéder, ezután létrehozza az új elemeket a következő szintre.

Vegyük n dimenziós poliéder elemekkel f i> (i dimenziós szembe. I = 0. n). Prismatic (n + 1) dimenziós poliéder lesz 2 f i + f - 1 + F_> dimenzió elemei i (az F - 1 = 0 0 => f n = 1 1 =>.).

• Vegyünk egy sokszög n csúcsú és n oldalról. Kapunk prizma 2 n csúcsú, 3n élek és 2 + n metszettel.
• Vegyünk egy poliéder v csúcsok, e élek, és f arcok. Kapunk (4-dimenziós) prizma csúcsot 2v 2 e + V bordák 2 f + e 2 arcok és + F sejtek.
• Vegyük a négydimenziós poliéder csúcsai v, e élek, f c aspektusát és sejteket. Beszerzése (5-dimenziós) prizma csúcsot 2v 2 e + V bordák 2 F + E (2-dimenziós) arcok, c + f 2 és a sejtek 2 + c giperyacheykami.

Homogén prizmás polyhedra

Szabályos n poliéder által képviselt Schläfli p. q. t>, képezhet egy homogén poliéder prizma dimenzió (n + 1) által képviselt közvetlen terméke két Schläfli szimbólumok. o. q. t> ×<>.

• Prism 0-dimenziós poliéder - egy szegmens. képviseli a null karakter Schläfli <>.
• Prism 1 dimenziós poliéder - egy téglalap. nyert két szegmens. Ez a prizma kerül bemutatásra, mint a munka Schläfli szimbólumok <>×<>. Ha a prizma egy négyzet. rögzítés lehet csökkenteni: <>×<> =.
  • Példa: Square, <>×<>, Két párhuzamos vonal, csatlakozott a másik két szegmens, a felek.
• sokszögű hasáb - ez 3-dimenziós prizma, nyert két sokszög (egy kapott párhuzamos fordítása egy másik), amelyek össze vannak kötve téglalapok. Egy szabályos sokszög p> Van egy egységes n -ugolnuyu prizma termék által biztosított p> ×<>. Ha p = 4 prizma válik a kocka. ×<> =.
  • Példa: A ötszögű hasáb. ×<>, két párhuzamos ötszög csatlakoztatva öt derékszögű oldalán.
• Négy-dimenziós prizma, nyert két poliéderek (egy kapott párhuzamos fordítása a másik), a kötődését 3-dimenziós prizmatikus sejtek. A rendszeres poliéder p. q> lehet egy egységes 4-dimenziós prizma által biztosított termék o. q> ×<>. Ha a poliéder egy kocka, hasáb oldalon is kocka, hasáb alakul négydimenziós kockának. ×<> =.
  • Példa: dodeka prizma [en]. ×<>, két párhuzamos dodekaéder. csatlakoztatva ötszögű prizmák 12 (a felek).
• .

Prizmás poliéderek magasabb dimenziók is léteznek, mint a közvetlen terméke bármely két poliéder. A dimenziója prizmás poliéder a termék elemeit a termék méretei. Az első példa egy ilyen munka van egy 4-dimenziós térben úgynevezett duoprizmami. amelyeket úgy kapunk, a termék a két sokszög. Helyes duoprizmy bemutatott szimbólum p> × q>.

Csavart hasáb - egy nem-konvex poliéder prizma, nyert homogén -ugolnoy q elosztjuk az átlós a oldalfelületek és a forgatás a felső bázis, jellegzetesen egy szöget π Q >> radián (q >> 180 fok) abban az irányban, amelyben a fél válnak homorú [3 ] [4].

Csavart hasáb nem lehet bontani tetraéder anélkül, hogy új csúcsot. A legkisebb az esetben az ún poliéder Shonhardta.

Csavart hasáb topologikusan azonos antiprism. de a fél szimmetriák. Dn. [N, 2] +. rendelni 2n. Ez a prizma lehet tekinteni, mint egy domború antiprism, amelyben a tetraéderek eltávolított párok közötti háromszögek.

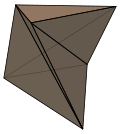
poliéder Shonhardta

Csavart négyzetes hasáb

négyzet antiprism

Szálú tizenkétszögű prizma