modul és egyenlőtlenségek
A modul valós szám - az abszolút értéke ez a szám. Egyszerűen fogalmazva, a rögzítő modul kikerül a számát a jel. jelöljük | a |. Például | 6 | = 6, | -3 | = 3, | -10,45 | = 10,45. Definíció modul A modul tulajdonságai
1) A modulok szemközti számok | a | = | -a |. 2) a szám a modul egyenlő a tér a tér ez a szám | a | 2 = a 2. 3) A négyzetgyöke egy négyzet egy moduljának ez a szám √ (2) = a 2. 4) A modul száma egy nem negatív szám | a | ≥ 0. 5) pozitív konstans tényező lehet venni a modulon kívüli jel | Ca | = c | a |, c> 0 6), ha | a | = | b |. akkor a = ± b. 7) Modul termék két (vagy több) a számok egyenlő a termék az abszolút értékeket | egy # 8729; b | = | a | # 8729; | b | .
A geometriai jelentése a modul A modul számát - a távolság nulla egy adott számot. Például, | -5 | = 5. Más szóval, a távolság a nulladik -5 5. Tekintsük a legegyszerűbb egyenlet | x | = 3 Láthatjuk, hogy a számegyenesen, van két pont, amelyek távolsága nulla egyenlő három. Ez a pont a 3. és -3. Tehát az egyenlet | x | = 3, két megoldás van: x = 3, és x = -3. A geometriai jelentését az értékek a különbség modul - a távolság közöttük. Például a geometriai kifejezés jelentését | x - a | - koordinátatengely hossza összekötő szakasz pontot a abszcisszán X és a. 1. példa: az egyenlet megoldásához: | x - 3 | = 4. megoldás. Ez az egyenlet lehet olvasni, mint a távolság x pont-pont a 3. 4. A grafikus módszerrel meg tudja határozni, hogy az egyenletnek két megoldás: 1 és 7: 1; 7. példa 2. Problémák egyenlőtlenséget: | x + 7 | <4. Решение. Можно прочитать как: расстояние от точки х до точки –7 меньше четырёх. Ответ: (-11; -3). Пример 3. Решить неравенство: |10 — x | ≥ 7. Решение. Расстояние от точки 10 до точки х больше или равно семи.
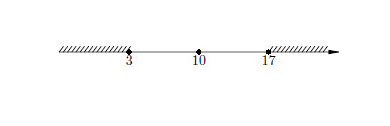
Válasz: (-∞; 3] υ [17, + ∞). Megjegyzés. Translation algebrai probléma geometriai nyelv gyakran elkerüli nehézkes. 4. példa megoldásához egyenletet. | x - 1 | + | x - 2 | = 1. megoldás. Mi a következőképpen kell eljárni: kezdve a geometriai értelmező modul bal oldalán az egyenlet képviseli a távolságok összege egy pont abszcissza x két fix pontot abszcisszavonal 1. és 2. akkor nyilvánvaló, hogy az összes pontot a abszcisszák, az [1; 2] rendelkezik a szükséges ingatlanok, valamint a pontok kívül található ebben a szegmensben - nem. Ezért a választ: a meghatározott megoldás van, az [1; 2]. Válasz: [1; 2]. 5. példa az egyenlet megoldásához: | x - 1 | - | x - 2 | = 1. megoldás. Hasonlóképpen, azt találjuk, hogy a különbség a távolságok a 1. és 2. pont abszcissza egyenlő egység csak a pontokat a jobb oldalon található koordináta tengelye 2. Akkor a válasz - ray [2; + ∞). Válasz: [2; + ∞). 6. példa megoldásához az | x + 1 | + | x - 1 |> 2. megoldás. Képviselni a koordináta tengelyen pont, az összeget, amelynek távolságok pontok -1 és 1 pontosan megegyezik 2. Ez a pont az intervallum [-1; 1]. Nyilvánvaló, hogy minden szám kívül intervallum távolságok összege nagyobb lesz, mint kettő, ahol a választ: (-∞, -1) (1; + ∞). Válasz: (-∞; -1) (1; + ∞). Megjegyzés. Általános megoldások A fenti egyenletek a következők átmenetek egyenlőek:
| X - a | + | X - b | = B - a, b ≥ egy, a ≤ x ≤ b | x - a | - | x - b | = B - a, b ≥ egy, x ≥ b
