Hogyan magyarázza, hogy a gyermek hosszú osztás
Az egyik legfontosabb lépés a tanítás a gyermek matematikai műveletek - képzési részleg működését prímszám. Hogyan magyarázza, hogy a gyermek részleg, ahol elkezdheti a fejlesztés ebben a témában?
Annak érdekében, hogy tanítani a gyermeket, hogy ossza meg kell, hogy abban az időben ő már elsajátította a tanulás ilyen matematikai műveletek, mint az összeadás, kivonás, és volt egy világos megértése a lényege az intézkedés szorzás és osztás. Ez azt jelenti, meg kell érteni, hogy a szétválás - egy részlege valamit egyenlő részre. Arra is szükség van, hogy tanítani a szorzás és megtanulják a szorzótábla.
Tanulási szétválasztási művelet (osztás) egy része a formájában a játék

Mondjuk, hogy 8 egyforma kockákra, és kérdezze meg gyermeke osztani két egyenlő részre - neki és egy másik férfi. Változhat, és bonyolítja a feladat, kérdezze meg gyermeke osztani a 8 kocka, mint két és négy ember. Elemezzük az eredményeket vele. Cserélje ki az alkatrészeket, akkor próbálkozzon egy másik objektumok számát, és az emberek, hogy kell osztani ezeket az elemeket.
Fontos: Győződjön meg arról, hogy a gyermek először működtetni páros számú elem, hogy a végeredmény az osztály volt az azonos számú részből áll. Ez hasznos lesz a következő fázis, amikor a gyermek meg kell érteni, hogy a szétválás - egy művelet fordítottja szorzás.
Szaporodnak és osztódnak a szorzótábla
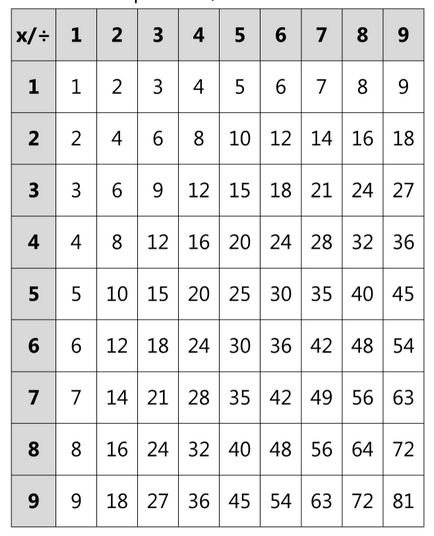
Magyarázza el gyermekének, hogy a matematika, a cselekvéstől, amely ellentétes a szorzás az úgynevezett „osztály”. Feltételek szorzótábla, bizonyítani a tanuló például kapcsolatát szorzás és osztás.
Példa: 4x2 = 8. Emlékeztetni kell a gyermeket, hogy a szorzata a termék két szám. Ezt követően kifejtik, hogy a szétválás művelet fordítottja a szorzás művelet, és illusztrálja ezt világosan.
Osszuk a kapott termék a „8” példa - bármely, a faktorok - „2” vagy „4”, és az eredmény mindig más, nem használt a műveletben tényező.
Mozgás tovább vizsgálva más példák szorzótábla.
Sőt, meg kell tanítani a gyermeket szorzótábla „éppen ellenkezőleg”, és emlékezni kell, valamint a szorzótábla is, mert szükség lesz, amikor elkezdi tanulni hosszú részlege.
Osszuk a hasáb - gyorsan és egyszerűen
világosan megmagyarázni
Osszuk 938 által a 7. Ebben a példában 938 - osztható, 7 - térelválasztó. Az eredmény az lesz saját, és ki kell számítani.
1. lépés: Írja be a számot elosztjuk a „terület”.
2. lépés megjelenítése tanítványa az osztalék és megkéri, hogy válasszon a közül a legkisebb szám, amely nagyobb, mint az osztó. Három számjegy 9, 3 és 8, ez a szám 9. Ösztönözni kell a gyermeket, hogy elemezze, hányszor száma 7 lehet jelen a 9-es szám? Ez igaz, csak egyszer. Ezért először felvettük az eredmény 1.
Lépés 3. Menj a regisztrációs hosszú osztály:
Szorzás elválasztó szerezni 7H1 és 7. kapott eredményt az első rekord számú osztalékpolitikánknak 938 és kivonni, mint mindig, egy oszlopra. Vagyis, mi kivonni 9 7 és kap 2.
4. lépés: Az a szám, hogy látjuk kevesebb, mint az osztó, így meg kell, hogy növelni kell. Ehhez kombinálni a következő szabad szám a mi osztalék - ez kerül jóváírásra 3. 3. a kapott szám 2.
5. lépés: Ezután hatnak a már jól ismert algoritmus. Elemezzük, hogy mennyi idő a térelválasztó 7 tartalmazza a kapott szám 23? Ez így van, háromszor. Mi rögzíti a 3-as számú magán. A végeredmény a termékről - 21 (7 * 3) számos rekord 23 alatt egy oszlopra.
Shag.6 Most meg kell találnunk az utolsó szám a mi saját. Az ismerős algoritmus, továbbra is a számításokat az oszlop. Kivonással az oszlop (23-21) fogadja a különbség. Ez egyenlő 2.
Az osztalék mi marad kihasználatlan egy számot - 8 kombinálja azt, hogy kivonásával kapott 2-es szám, megkapjuk - 28.
Shag.7 elemzése mennyi időt mi elválasztó 7 tartalmazza a kapott szám? Ez így van, 4-szer. Rögzíti a kapott számjegy, mint az eredmény. Tehát, kaptunk eredményeként hosszú osztás hányadosa = 134.
A legfontosabb dolog, amikor tanítani a gyermeket hosszú részlege, az asszimiláció az algoritmus, ami általában igen egyszerű.
Ha a gyermek jól működik a szorzótábla, és a „fordított” osztály, ő nem lesz nehézség. Mindazonáltal fontos, hogy folyamatosan képezzük a frissen tanultakat. Ne hagyja ott, amint észreveszi, hogy a gyerek elkapta a módszer lényege.
Annak érdekében, hogy könnyen tanítani a gyermeket az osztási művelet szükséges:
A tanulmány a matematika hozta a gyermek móka, meg kell, hogy gerjeszti az érdeklődését a matematika és a matematikai műveleteket, és nem csak a képzés során, hanem a mindennapi helyzetekben.
Ezért, hogy támogassák és fejlesszék a gyermek megfigyelés, hogy analógiát vonhatunk matematikai műveletek (műveletek a fiókot, és osztás, kapcsolatok elemzésére „rész-egész”, stb) az építés során, a játékok és a természet megfigyelése.