Hogyan lehet megoldani az egyenletet, amelynek modulusa

Egyenlet egy modulusa (abszolút érték) bármely olyan egyenlet, amelyben a variábilis vagy expressziós zárják egy moduláris zárójel. Az x abszolút értéke jelöli | x | . és a modul mindig pozitív (kivéve a zérus, amely se nem pozitív, se nem negatív szám). Az egyenletet megoldani az abszolút érték, mint bármely más matematikai egyenlet, de az egyenlet a modul két a végeredmény, mert szükséges, hogy megoldja az egyenletet a pozitív és negatív.

lépések szerkesztése

1. rész 3: Felvétel szerkesztése egyenlet

Fogalmának megértése abszolút értékének geometriai szempontból. A modul száma egyenlő a távolság a származási és ez a szám. [2] A modulként kialakított moduláris idézetek, amelyben egy szám, változó, vagy expressziós (| x |). A modul száma mindig pozitív. [3]

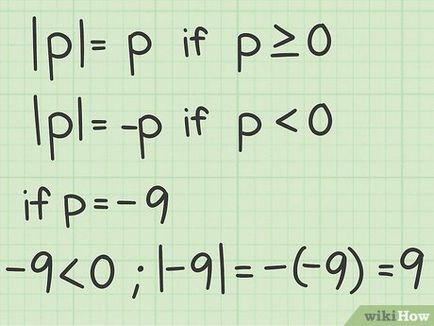
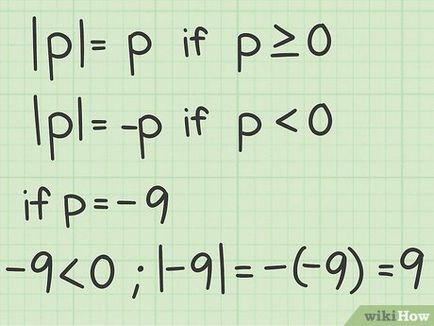
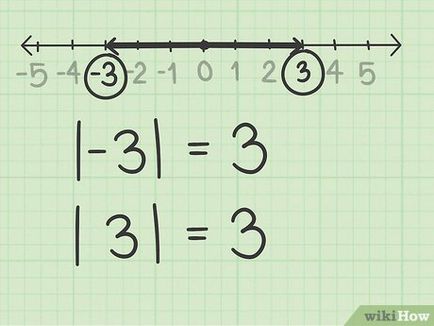
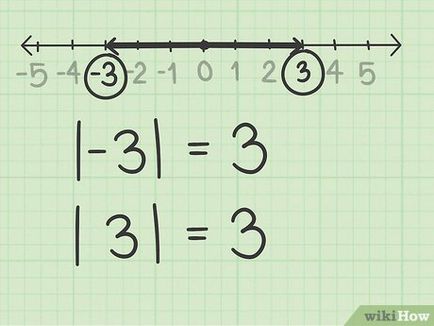
• Például | - 3. | = 3 | 3. | = 3. Mind a számok -3 és 3 a parttól három egység 0.

Az egyenletben elkülöníteni modult. Abszolút értéke legyen az egyik oldalon az egyenlet. Bármennyi vagy tagok moduláris zárójelben kell mozgatni a másik oldalon az egyenlet. [4] Megjegyzendő, hogy az egység nem lehet beállítani, hogy egy negatív szám, ezért ha az izolálás után modul, ez egy negatív szám, ez az egyenlet nincs megoldása. [5]

• Például, mivel az egyenlet | 6 x - 2 | + 3 = 7; elkülöníteni az egység mindkét oldalán az egyenlet, kivonni 3:
  | 6 x - 2 | + 3 = 7
  | 6 x - 2 | + 3 - 3 = 7 - 3
  | 6 x - 2 | = 4

Ellenőrizze az eredmény pozitív megoldása az egyenletnek. Erre kapott értéket helyettesítse az eredeti egyenlet [8]. vagyis helyettesítse az x értékét. következtében talált pozitív egyenlet megoldásai az eredeti egyenlet a modullal. Ha az egyenlőség, a döntés joga.

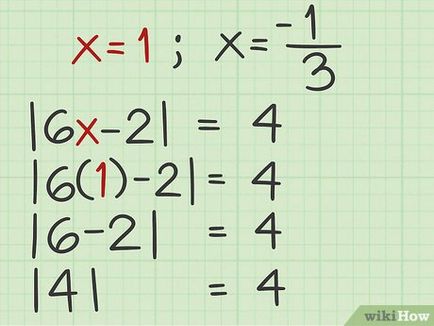
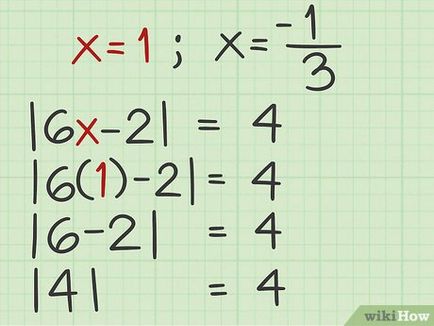
• Például, ha ennek eredményeként a pozitív egyenlet megoldása úgy találja, hogy az x = 1. helyettesíti az eredeti egyenlet 1:
  | 6 x - 2 | = 4
  | 6 (1) - 2 | = 4
  | 6-2 | = 4
  | 4 | = 4

Ellenőrizze az eredményt az elutasító határozat az egyenlet. Ha egyik megoldás helyes, ez nem jelenti azt, hogy a második döntés helyes. Ezért, hogy helyettesítse az x értékét. talált megoldása az egyenletnek negatív, az eredeti egyenlet a modullal.

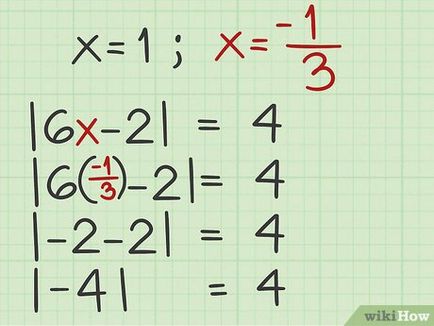
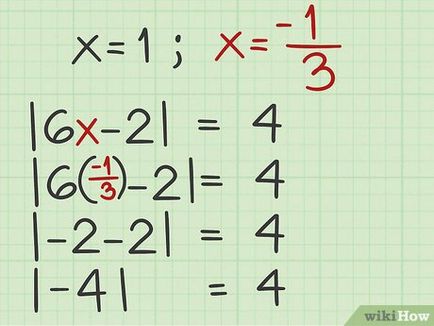
• Például, ha ennek eredményeként az elutasító határozat az egyenlet úgy találja, hogy az x = - március 1 >>. helyettesítő - 1 3 >> az eredeti egyenletet:
  | 6 x - 2 | = 4
  | 6 (- 1 3) - 2 | = 4>) - 2 | = 4>
  | - 2-2 | = 4
  | - 4 | = 4

Ügyeljen arra, hogy valós megoldásokat. Az egyenlet megoldása érvényes (igaz), ha a helyettesítés az eredeti egyenlet figyelhető ravenstvo.Imeyte arra, hogy az egyenlet két, egy vagy nincs igazi megoldás.

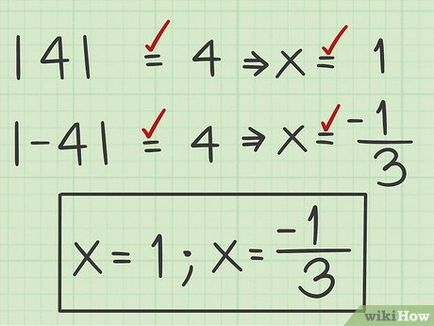
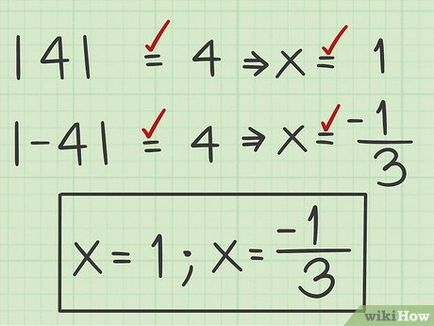
• Ebben a példában | 4 | = 4 és | - 4 | = 4. azaz az egyenlő mindkét megoldás érvényesek. Így az egyenlet | 6 x - 2 | + 3 = 7 két lehetséges megoldás: x = 1. x = - március 1 >>.