A módszer a szakaszok - studopediya
Módszer szakaszok mentális test boncolás síkban tekintve egyensúlyi vagy kimetszett cha stey.
Ha az egész test egyensúlyban van, és minden egyes rész egyensúly van az intézkedés alapján a külső és belső erők. A belső erők meghatározzuk az egyenletek az egyensúlyi, a készítmény-képviselt az adott testrészre.
Boncoló test keresztirányú sík (ábra. 19.1). Úgy véljük, a jobb oldali. Rajta kívül vannak silyF4; F5; F6 és befelé beállított rugalmas erő Qc. elosztva a keresztmetszet. Elosztási rendszer, osztott erők helyettesítheti a fő vektora Ro. helyezni a súlypont a keresztmetszet, és a teljes nyomatékot.
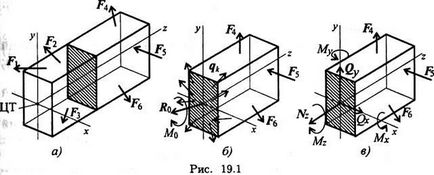
Bővítése a fő vektor Ro tengely, megkapjuk három összetevőből áll:
A lényeg az, szintén jelen formájában pontpárok hatalmi a három sík vetítés:
Az így kapott komponenseket a rugalmas erők nevezzük vnut-Nal teljesítmény tényezők. Mind a belső hatalmi facto árok okoz deformáció a terméket. Belső siló-TIONS tényezők egyensúlyát csatolt ezt az elemet de tali külső erők. Segítségével hat egyensúlyi egyenletek, tudunk szerezni a nagysága a belső hatalmi tényezők:
Ezekből az egyenletekből következik, hogy:
NZ - hosszirányú erő egyenlő az algebrai összege az előrejelzések tengelye Oz a külső erők hatnak a sérült részbe a fa; Ez okozza húzó vagy nyomó;
Qx - nyíróerő, amely egyenlő az algebrai összege a nyúlványok az x-tengelyen a külső erők hatnak a levágott rész;
Qy - nyíróerő, amely egyenlő az algebrai összege a nyúlványok az y-tengelyen a külső erők hatnak a levágott rész;
Mz - nyomaték megegyezik az algebrai összege mo-Greguss Pál külső erők a hosszanti tengelye Oz- okozza csavaró a fény;
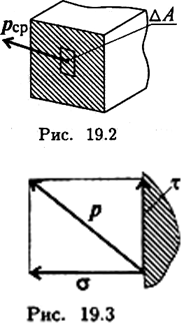
Mu - hajlítónyomaték egyenlő az algebrai összege mo-Ments a külső erők adott az y tengely.
Pillanatok Mx és My okozott gerendák meghajlítani a megfelelő gépet.